Prensa hidráulica
La prensa hidráulica es un mecanismo conformado por vasos comunicantes impulsados por pistones de diferentes áreas que, mediante una pequeña fuerza
sobre el pistón de menor área, permite obtener una fuerza mayor en el
pistón de mayor área. Los pistones son llamados pistones de agua, ya que
son hidráulicos. Estos hacen funcionar conjuntamente a las prensas
hidráulicas por medio de motores.
Antigua prensa hidráulica.
En el siglo XVII, en Francia, el matemático y filósofo Blaise Pascal comenzó una investigación referente al principio mediante el cual la presión aplicada a un líquido contenido en un recipiente se transmite con la misma intensidad en todas direcciones.1
Gracias a este principio se pueden obtener fuerzas muy grandes
utilizando otras relativamente pequeñas. Uno de los aparatos más comunes
para alcanzar lo anteriormente mencionado es la prensa hidráulica, la
cual está basada en el principio de Pascal.
El rendimiento de la prensa hidráulica guarda similitudes con el de la palanca,
pues se obtienen fuerzas mayores que las ejercidas pero se aminora la
velocidad y la longitud de desplazamiento, en similar proporción.
Cálculo de la relación de fuerzas
Cuando se aplica una fuerza sobre el émbolo de menor área
sobre el émbolo de menor área 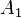 se genera una presión
se genera una presión  :
:
Esquema de fuerzas y áreas de una prensa hidráulica.
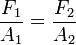 y la relación de fuerzas:
y la relación de fuerzas: 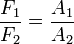
 = fuerza del émbolo menor en N.
= fuerza del émbolo menor en N.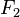 = fuerza del émbolo mayor en N.
= fuerza del émbolo mayor en N.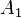 = área del émbolo menor en m².
= área del émbolo menor en m².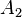 = área del émbolo mayor en m².
= área del émbolo mayor en m².- La prensa hidráulica es una máquina que
se basa en el principio
de Pascal para transmitir una fuerza.
Aprovechando que la presión es la misma, una
pequeña fuerza
sobre una superficie chica es equivalente a una fuerza grande
sobre una superficie también grande, proporcionalmente
iguales.
P1 = P2
P1, P2 = Presiones en 1 y en 2
F1, F2 = Fuerzas 1 y 2
S1, S2 = Superficies 1 y 2
Émbolos a distinta altura
Un ejercicio interesante, es el de determinar la altura de ambas columnas de fluido cuando se ponen n1 pesas en el émbolo de la izquierda y n2 pesas en el émbolo de la derecha.
Sean A y B dos puntos del fluido que están a la misma altura. El punto A una profundidad h1 por debajo del émbolo de área S1 y el B situado h2 por debajo del émbolo de área S2.
La presión en cada uno de dichos puntos es la suma de tres términos
- La presión atmosférica
- La presión debida a la columna de fluido
- La presión debida a las pesas situadas sobre el émbolo
Para determinar h1 y h2 en función de los datos n1 y n2, precisamos de dos ecuaciones
La primera ecuación es pA=pB
La segunda ecuación, nos indica que el fluido incomprensible pasa de un recipiente al otro, pero el volumen V de fluido permanece invariable. Por ejemplo, si h1 disminuye, h2 aumenta. Como consecuencia, el fluido pasa del recipiente izquierdo al derecho, hasta que se establece de nuevo el equilibrio.
Donde h0 es la altura inicial de equilibrio.
Ejemplo:
Ponemos tres pesas en el émbolo de la izquierda, y ninguna pesa en el émbolo de la derecha, n1=3, n2=0. El émbolo izquierdo baja y sube el émbolo derecho.
- Sea el radio del émbolo de la izquierda r1=5 cm=0.05 m
- El radio del émbolo de la derecha r2=10 cm=0.1 m
- La altura inicial de equilibrio es h0=20 cm=0.2 m
- La densidad del agua es ρ=1000 kg/m3
- La masa m de cada una de las pesas es 250 g=0.25 kg.
- La presión atmosférica p0 se simplifica en la primera ecuación
- Igualdad de presiones a la misma altura pA=pB
- El agua pasa del recipiente izquierdo al recipiente derecho, pero el volumen total de fluido permanece invariable
La solución es h1=0.124 m=12.4 cm y h2=0.219 m=21.9 cm


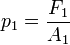
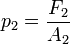
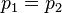

No hay comentarios:
Publicar un comentario