Densidad
En física y química, la densidad (del latín densĭtas, -ātis) es una magnitud escalar referida a la cantidad de masa en un determinado volumen de una sustancia. Usualmente se simboliza mediante la letra rho ρ del alfabeto griego. La densidad media es la razón entre la masa de un cuerpo y el volumen que ocupa.
Si un cuerpo no tiene una distribución uniforme de la masa en todos
sus puntos la densidad alrededor de un punto puede diferir de la
densidad media. Si se considera una sucesión pequeños volúmenes
decrecientes 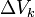 (convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo
(convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo  la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
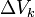 (convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo
(convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo  la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
Como ejemplo, un objeto de plomo es más denso que otro de corcho, con independencia del tamaño y masa.

Un cilindro graduado que contiene varios líquidos de colores con diferentes densidades.
Densidad absoluta
La densidad o densidad absoluta es la magnitud que expresa la relación entre la masa y el volumen de una sustancia. Su unidad en el Sistema Internacional es kilogramo por metro cúbico (kg/m³), aunque frecuentemente también es expresada en g/cm³. La densidad es una magnitud intensiva. , la densidad; m, la masa; y V, el volumen de la sustancia.
, la densidad; m, la masa; y V, el volumen de la sustancia.Densidad relativa
La densidad del aire frente a la temperatura.
donde 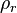 es la densidad relativa,
es la densidad relativa,  es la densidad de la sustancia, y
es la densidad de la sustancia, y  es la densidad de referencia o absoluta.
es la densidad de referencia o absoluta.
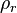 es la densidad relativa,
es la densidad relativa,  es la densidad de la sustancia, y
es la densidad de la sustancia, y  es la densidad de referencia o absoluta.
es la densidad de referencia o absoluta.
Para los líquidos y los sólidos, la densidad de referencia habitual es la del agua líquida a la presión de 1 atm y la temperatura de 4 °C. En esas condiciones, la densidad absoluta del agua destilada es de 1000 kg/m³, es decir, 1 kg/dm³.
Para los gases, la densidad de referencia habitual es la del aire a la presión de 1 atm y la temperatura de 0 °C.
Densidad media y densidad puntual
Para un sistema homogéneo, la expresión masa/volumen puede aplicarse en cualquier región del sistema obteniendo siempre el mismo resultado.
Sin embargo, un sistema heterogéneo no presenta la misma densidad en
partes diferentes. En este caso, hay que medir la "densidad media",
dividiendo la masa del objeto por su volumen o la "densidad puntual" que
será distinta en cada punto, posición o porción "infinitesimal" del sistema, y que vendrá definida por:
Sin embargo, debe tenerse que las hipótesis de la mecánica de medios continuos solo son válidas hasta escalas de 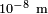 , ya que a escalas atómicas la densidad no está bien definida. Por ejemplo, el tamaño del núcleo atómico es cerca de
, ya que a escalas atómicas la densidad no está bien definida. Por ejemplo, el tamaño del núcleo atómico es cerca de 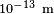 y en él se concentra la inmensa mayor parte de la masa atómica, por lo que su densidad (2,3·1017 kg/m3)
es muy superior a la de la materia ordinaria. Es decir, a escala
atómica la densidad dista mucho de ser uniforme, ya que los átomos están
esencialmente vacíos, con prácticamente toda la masa concentrada en el
núcleo atómico.
y en él se concentra la inmensa mayor parte de la masa atómica, por lo que su densidad (2,3·1017 kg/m3)
es muy superior a la de la materia ordinaria. Es decir, a escala
atómica la densidad dista mucho de ser uniforme, ya que los átomos están
esencialmente vacíos, con prácticamente toda la masa concentrada en el
núcleo atómico.
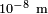 , ya que a escalas atómicas la densidad no está bien definida. Por ejemplo, el tamaño del núcleo atómico es cerca de
, ya que a escalas atómicas la densidad no está bien definida. Por ejemplo, el tamaño del núcleo atómico es cerca de 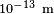 y en él se concentra la inmensa mayor parte de la masa atómica, por lo que su densidad (2,3·1017 kg/m3)
es muy superior a la de la materia ordinaria. Es decir, a escala
atómica la densidad dista mucho de ser uniforme, ya que los átomos están
esencialmente vacíos, con prácticamente toda la masa concentrada en el
núcleo atómico.
y en él se concentra la inmensa mayor parte de la masa atómica, por lo que su densidad (2,3·1017 kg/m3)
es muy superior a la de la materia ordinaria. Es decir, a escala
atómica la densidad dista mucho de ser uniforme, ya que los átomos están
esencialmente vacíos, con prácticamente toda la masa concentrada en el
núcleo atómico.Densidad aparente
La densidad aparente es una magnitud aplicada en materiales de constitución heterogénea, y entre ellos, los porosos como el suelo,
los cuales forman cuerpos heterogéneos con intersticios de aire u otra
sustancia, de forma que la densidad total de un volumen del material es
menor que la densidad del material poroso si se compactase. En el caso
de un material mezclado con aire se tiene:
La densidad aparente de un material no es una propiedad intrínseca
del material y depende de su compactación. La densidad aparente del
suelo ( ) se obtiene secando una muestra de suelo de un volumen conocido a 105 °C hasta peso constante.
) se obtiene secando una muestra de suelo de un volumen conocido a 105 °C hasta peso constante.
 ) se obtiene secando una muestra de suelo de un volumen conocido a 105 °C hasta peso constante.
) se obtiene secando una muestra de suelo de un volumen conocido a 105 °C hasta peso constante.
Donde:
- WSS, Peso de suelo secado a 105 °C hasta peso constante.
- VS, Volumen original de la muestra de suelo.
Se debe considerar que para muestras de suelo que varíen su volumen
al momento del secado, como suelos con alta concentración de arcillas 2:1, se debe expresar el contenido de agua que poseía la muestra al momento de tomar el volumen.
En construcción se considera la densidad aparente de elementos de
obra, como por ejemplo de un muro de ladrillo, que contiene ladrillos,
mortero de cemento o de yeso y huecos con aire (cuando el ladrillo es
hueco o perforado).
Cambios de densidad
En general, la densidad de una sustancia varía cuando cambia la presión o la temperatura, y en los cambios de estado. En particular se ha establecido empíricamente:
- Cuando aumenta la presión, la densidad de cualquier material estable también aumenta.
- Como regla general, al aumentar la temperatura, la densidad disminuye (si la presión permanece constante). Sin embargo, existen notables excepciones a esta regla. Por ejemplo, la densidad del agua dulce crece entre el punto de fusión (a 0 °C) y los 4 °C; algo similar ocurre con el silicio a bajas temperaturas.[cita requerida]
El efecto de la temperatura y la presión en los sólidos y líquidos es muy pequeño, por lo que típicamente la compresibilidad de un líquido o sólido es de 10−6 bar−1 (1 bar=0,1 MPa) y el coeficiente de dilatación térmica es de 10−5 K−1. Las consideraciones anteriores llevan a que una ecuación de estado para una substancia ordinaria debe satisfacer las siguientes restricciones:
Por otro lado, la densidad de los gases es fuertemente afectada por la presión y la temperatura. La ley de los gases ideales describe matemáticamente la relación entre estas tres magnitudes:
donde  es la constante universal de los gases ideales,
es la constante universal de los gases ideales,  es la presión del gas,
es la presión del gas,  su masa molar y
su masa molar y 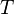 la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm
duplicará su densidad si se aumenta la presión a 2 atm manteniendo la
temperatura constante o, alternativamente, se reduce su temperatura a
150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()
la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm
duplicará su densidad si se aumenta la presión a 2 atm manteniendo la
temperatura constante o, alternativamente, se reduce su temperatura a
150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()
 es la constante universal de los gases ideales,
es la constante universal de los gases ideales,  es la presión del gas,
es la presión del gas,  su masa molar y
su masa molar y 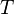 la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm
duplicará su densidad si se aumenta la presión a 2 atm manteniendo la
temperatura constante o, alternativamente, se reduce su temperatura a
150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()
la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm
duplicará su densidad si se aumenta la presión a 2 atm manteniendo la
temperatura constante o, alternativamente, se reduce su temperatura a
150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()Medición
Un densímetro automático que utiliza el principio del tubo en U oscilante.
La densidad puede obtenerse de forma indirecta y de forma directa.
Para la obtención indirecta de la densidad, se miden la masa y el
volumen por separado y posteriormente se calcula la densidad. La masa se
mide habitualmente con una balanza,
mientras que el volumen puede medirse determinando la forma del objeto y
midiendo las dimensiones apropiadas o mediante el desplazamiento de un
líquido, entre otros métodos. Los instrumentos más comunes para medir la
densidad son:
- El densímetro, que permite la medida directa de la densidad de un líquido.
- El picnómetro, que permite la medida precisa de la densidad de sólidos, líquidos y gases (picnómetro de gas).
- La balanza hidrostática, que permite calcular densidades de sólidos.
- La balanza de Mohr (variante de balanza hidrostática), que permite la medida precisa de la densidad de líquidos.
Otra posibilidad para determinar las densidades de líquidos y gases
es utilizar un instrumento digital basado en el principio del tubo en U
oscilante. Cuyo frecuencia de resonancia está determinada por los
materiales contenidos, como la masa del diapasón es determinante para la
altura del sonido.
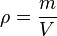
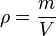

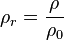

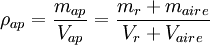
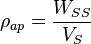
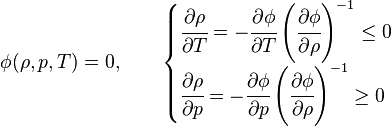
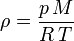


No hay comentarios:
Publicar un comentario